Contents

• Random Paving Patterns
• Regular Paving
• Random Paving
• Random Gradient of Paving
• Paving from Noise
• Hexagonal Paving from Noise
• Pathway from Noise

---

Random Paving Patterns

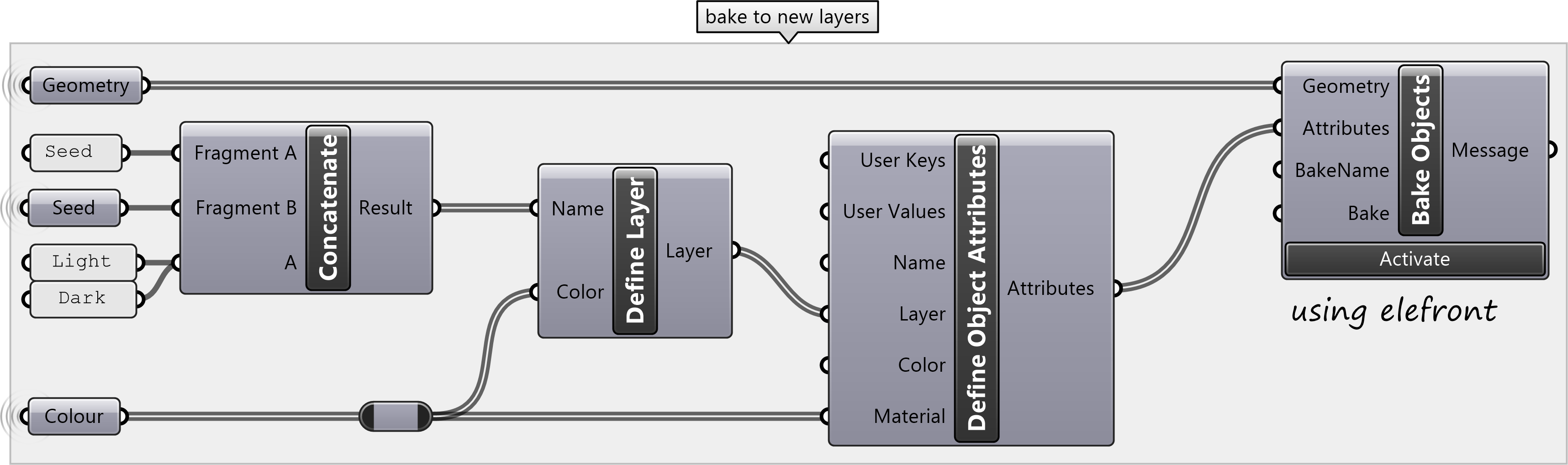
Download the Grasshopper definition for this tutorial.

Readings

• Patricio Gonzalez Vivo & Jen Lowe, 2015. Random, The Book of Shaders.
• Patricio Gonzalez Vivo & Jen Lowe, 2015. Noise, The Book of Shaders.
• Stefan Gustavson, 2005. Simplex Noise Demystified.

---

Regular Paving

---

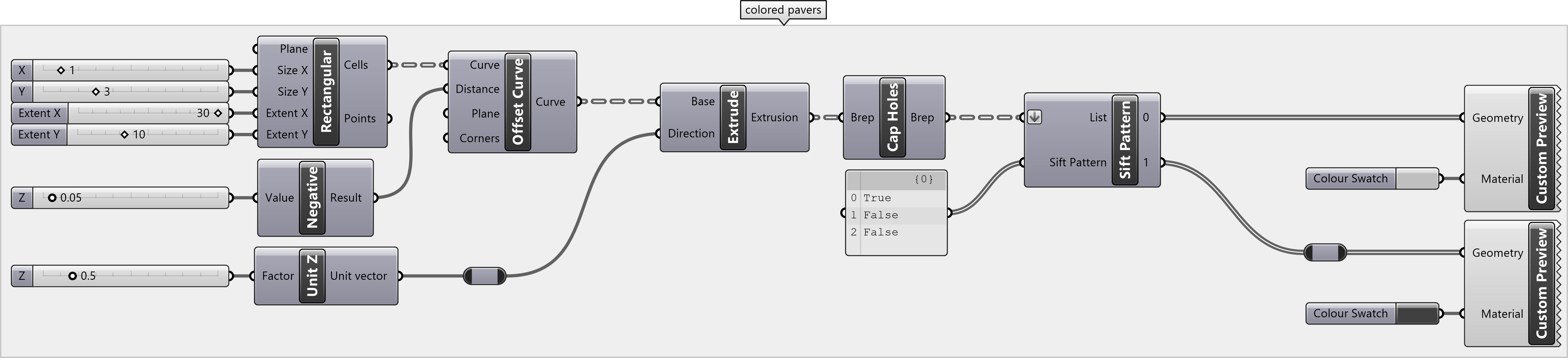
Random Paving

---

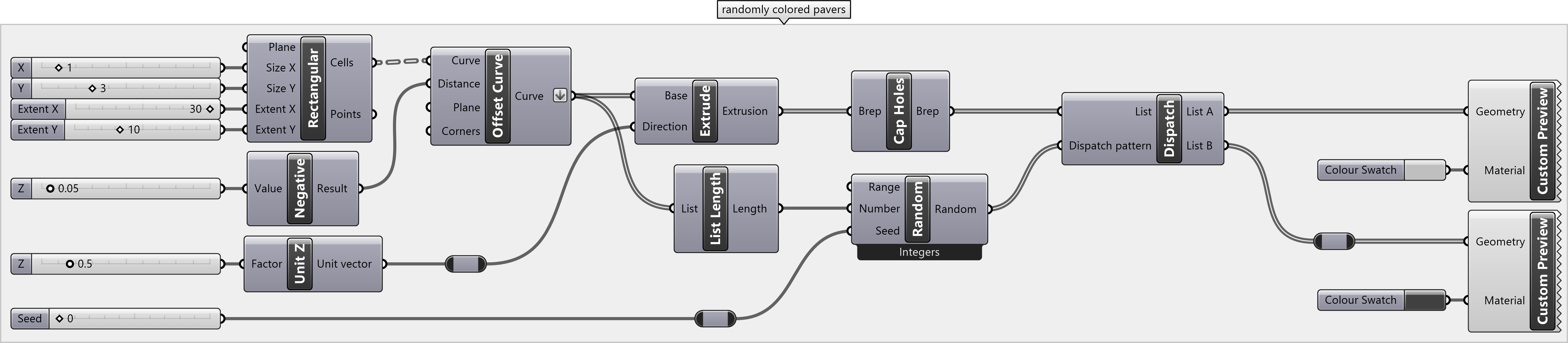
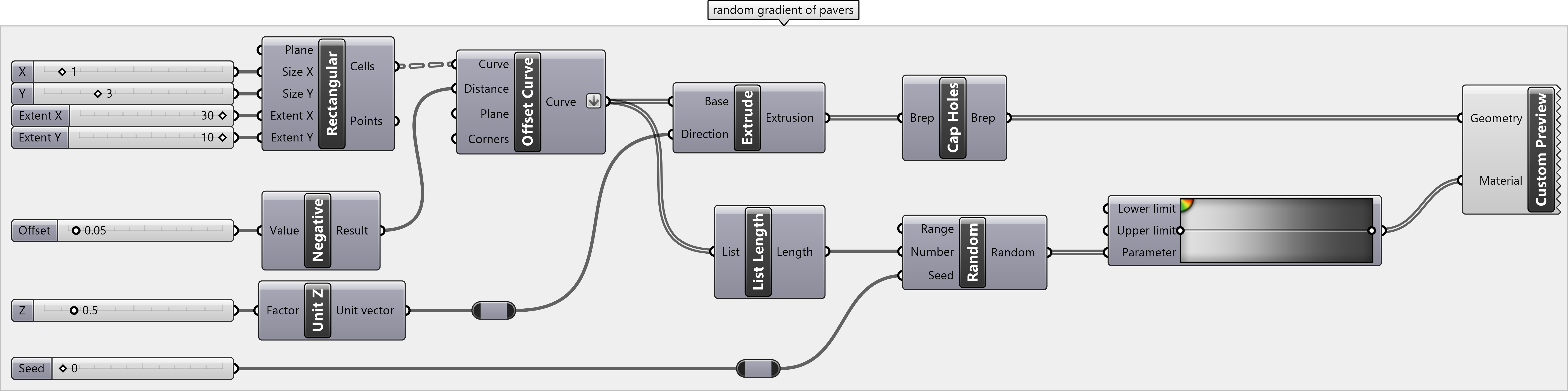
Random Gradient of Paving

---

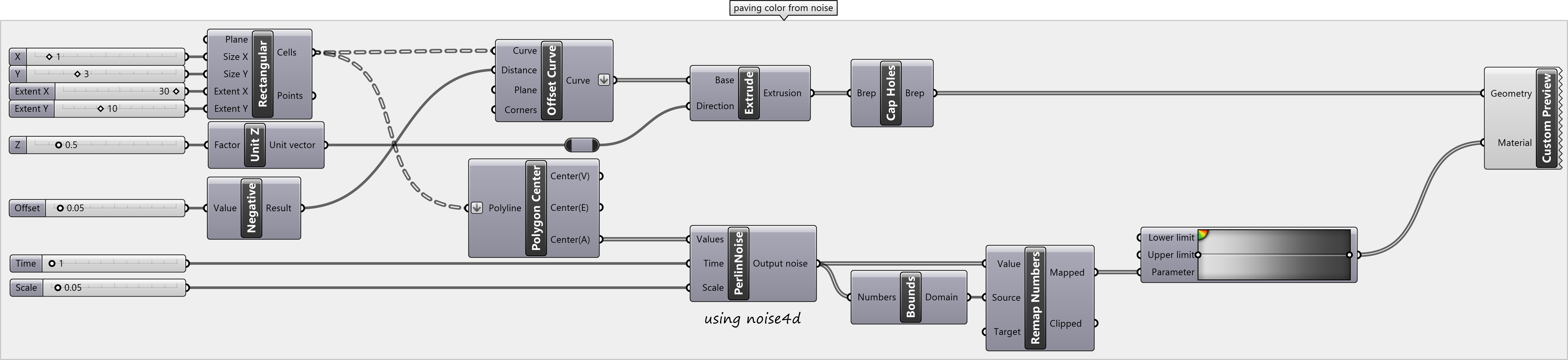
Paving from Noise

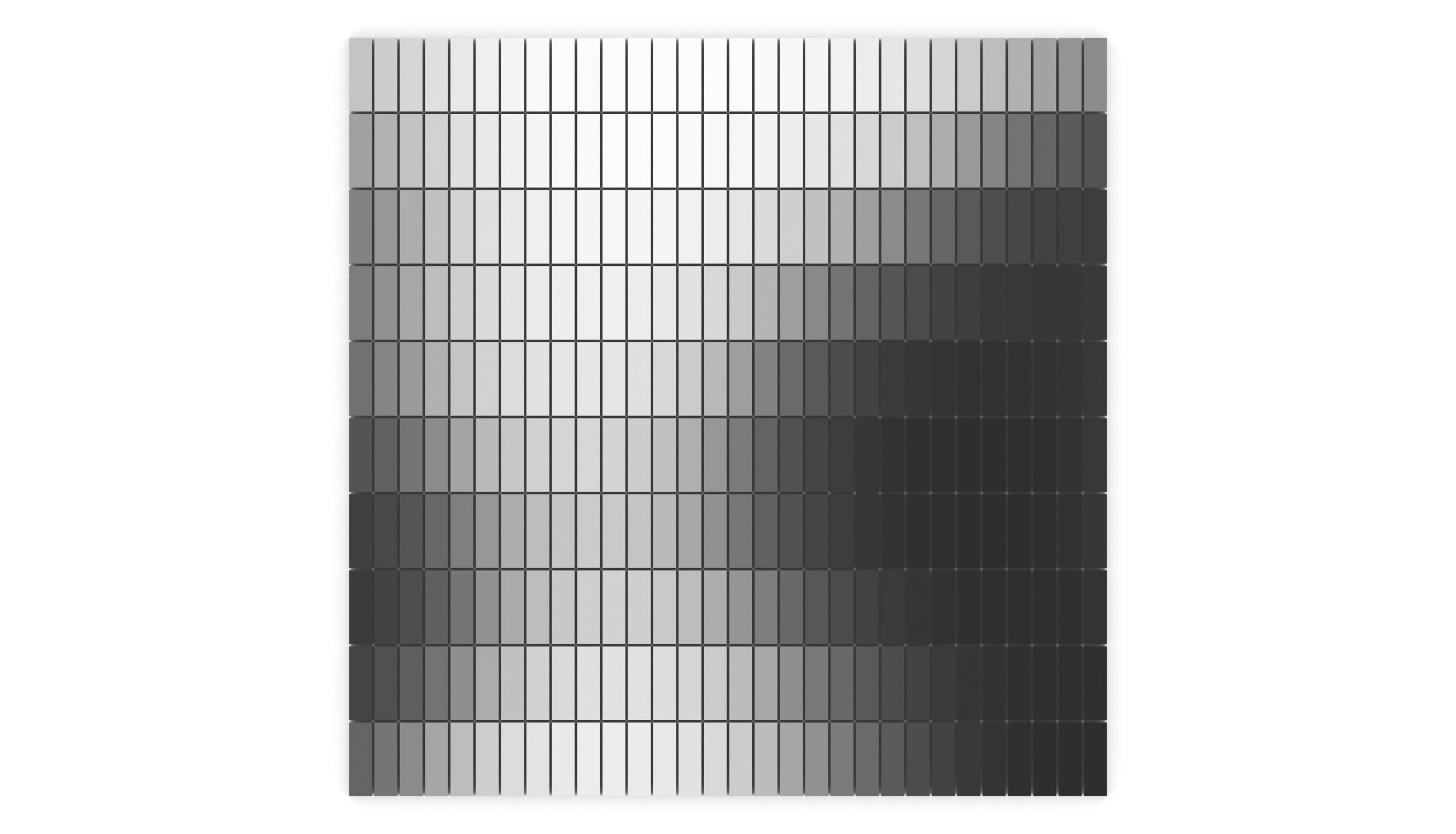
Noise is variation from an ideal signal. It is used in computer graphics to generate textures that appear pseudo-random, yet have a consistent scale of detail. Noise is often used to represent organic surfaces like topography, natural textures like marble, and natural phenomena like clouds. Perlin noise is created by interpolating between points in a grid with pseudo-random gradients. Use the Perlin or Simplex noise component from the 4D Noise addon to assign a color gradient to a grid of pavers. Create a rectangular grid, flatten the resulting tree of cells, and find the center of each cell with the polygon center component. Input the center of the cells as the values for Perlin Noise and then add time and scale parameters. Use remap numbers to rescale the noise values for a color gradient. Set the source domain to the bounds of the noise and set the target domain from 0 to 1. Alternatively, deconstruct the domain of the noise with deconstruct domain to set the lower and upper limits of the color gradient. Experiment with noise’s time and scale parameters to generate new patterns.

---

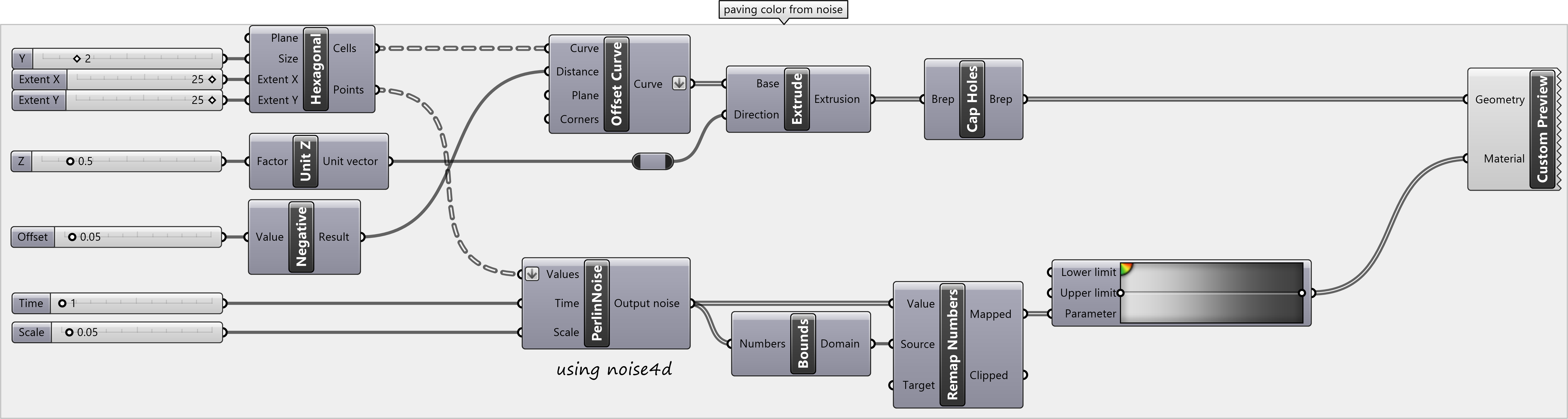
Hexagonal Paving from Noise

Generate a hexagonal paving pattern from noise by replacing the rectangular component with a hexagonal component. Use the center points of the hexagonal cells as the input values for the noise.

---

Pathway from Noise

Create a pathway from noise by using a culling pattern to hide pavers with a noise value greater than a given threshold. Filter the list of pavers with cull pattern and set the culling pattern to larger than a threshold. Adjust the parameters of the Perlin noise component to form a connected pathway.